SOLID STATE

Solid State

Key Terms students should be familiar with, in this chapter:

Crystalline	Amorphous	Space Lattice
Unit Cell	Simple Cube	Face Centered Cube fcc
Body Centered Cube bcc	Rock salt	Caesium chloride type
Zinc Blende	Fluorite	Antifluorite
Tetrahedral Void	Octahedral Void	Hexagonalclosepacking hcp
Cubic close packing ccp	Coordination number	Radius ratio
Ionic radii	Ortho silicates	Pyro silicates
Cyclic or ring silicates	Sheet silicates	3D Silicates
Point defects	Schotky defect	Frenkel defect
F-Centres	Dislocation	Conductors
Insulators	Semiconductors	Diamagnetic
Paramagnetic	Ferromagnetic	Spinels
Dielectric	Piezo electricity	Pyro electricity
Ferro electricity	Antiferro electricity	Super conductivity
12-16 Compounds	13-15 Compounds	Amphiboles
Pyroxenes	Radius ratio effect	N-Type of conductors
P-Type of conductors	Semiconductors	Photovoltaics - Transducers

Classification of Solids:

Ionic	Molecular	Covalent	Metallic
Positive and Negative ions	Molecules	Atoms	Positive metal kernels and free electrons
Strong Electrostatic forces of attraction	Van der Waals forces	Covalent bonds	Cohesive forces are electrostatic attraction or Metallic bonds
KCl, NaNO₃, CaF₂	Dry ice CO₂, CH₄, Sugar, Sulphur	Diamond, Silicon Carbide, graphite	Gold, Silver, Copper etc.
High m.p, b.p	Low m.p, b.p	High m.p	High m.p, b.p

Classification of solids:

Molecular Solids: The forces of attraction holding the molecules are Van der Waals forces. Examples of molecular Crystals are Ice, Solid Carbon dioxide, Sulphur, CH₄ , Wax.

Ionic Solids: The forces of attraction holding the ions together is electrostatic in nature. Examples are NaCl, BaCl₂, CsCl, NaNO₃ etc.

Covalent Solids: The binding forces are Covalent Bonds eg. Diamond, Silicon Carbide, Quartz.

Metallic Solids: The binding forces are electrostatic attraction eg. Copper, Aluminium, Silver, Gold etc.

Closed Packed Structures

In a crystal the constituent units atoms ions or molecules are arranged in such a way that the arrangement has minimum energy and thus maximum stability.

For maximum stability the constituent units in the crystal must be srrounded by maximum number of neighbours.

Three-dimensional packing of spheres

Hexagonal Close Packing hcp:- The spheres are arranged in a way such that the third layer comes vertically above the first layer the sequence may be represented as ABABABABA....... This type of arrangement is called hexagonal close packing or hcp arrangement e.g. Beryllium, Calcium, Cadmium, Zinc etc.

Cubic Close Packing ccp:- The spheres are arranged in a way such that the fourth layer comes vertically above the first layer. The sequence may be represented as ABCABCABC....... This type of arrangement is called cubic close packing or ccp arrangement.

The A,B,C represent the different layers of spheres in a three dimensional arrangement where each layer has a hexagonal close packing in 2 - dimension.

Voids

When arranging atoms in a 3D pattern there is space still unoccupied and these are regarded as holes or voids or interstices.

Tetrahedral Voids:- These are voids formed by 4 closely touching spheres.

Or one sphere resting on three touching spheres. It is called a tetrahedral void because the centres of the 4 touching are placed at the corners of a tetrahedra

Octahedral Voids:- These are voids formed by six touching spheres.

Or Three spheres belonging to one layer and three spheres belonging to the second layer. The centres of these spheres form a regular Octahedron.

Note 1. Octahedral Voids are bigger than Tetrahedral voids

2. Number of Octahedral voids are equal to the number of spheres

3. Number of Tetrahedral voids are equal to twice the number of spheres

4. Relationship between size of the voids and spheres is

a) Radius of atom ‘r’ in a Tetrahedral void = .225 R

b) Radius of atom ‘r’ in an Octahedral void = .414 R

Where R is the radius of the sphere in the close packing arrangement.

Co-ordination Number:- The total number of nearest neighbours, atoms or ions of a particular atom or ion in a crystal lattice is called co-ordination number.

Unit Cell:-

The smallest portion of a space lattice which generates the whole crystal by repeating its own dimensions in various directions is called unit cell

The smallest repeating unit in space lattice which when repeated over and over again produces the complete space lattice.

Structures of simple ionic compounds:

Crystal Structure	A brief detail with examples	Co-rdination Number	Formula units per unit Cell
NaCl -Type Rock-Salt	Na⁺ ions occupy the *Octahedral sites while Cl^-* ions are in ccp arrangement or *vice versa* eg. NH₄Cl, AgCl, AgBr, Halides of Li, Na &Rb; CaC₂ etc.	Na⁺ = 6 Cl^- = 6	4
CsCl-Type	Cs⁺ ions occupy *cubic sites* while Cl^- ions are at the *corners of a cube* or vice versa.	Cs⁺ = 8 Cl^- = 8	1
CaF₂ - Type Fluorite Structure	Ca²⁺ ions are in ccp while F^- ions occupy *Tetrahedral* sites e.g. CaF₂, BaF₂, BaCl₂, SrF₂ etc.	Ca²⁺ = 8 F ^- = 4	4
ZnS-Type a) Zinc blende	Zn²⁺ ions occupy Alternate tetrahedral sites e.g. while S²^- ions are in the ccp e.g. ZnS, CuCl, CuBr,CuI, AgI etc.	Zn²⁺ = 4 S^2- = 4	4
b) Wurzite	Zn²⁺ ions occupy Alternate tetrahedral sites while S^2- ions are in *hcp* type of arrangement.	Zn²⁺ = 4 S^2- = 4	4
Antifluorite Structure Na₂O	Positive ions occupy all the *tetrahedral sites while Negative ions are in ccp* type of arrangement. e.g. Na₂O	Na⁺ = 4 O^2- = 8	4

Types of Unit Cells:-

Simple Cubic Unit Cell: It is that unit cell in which the lattice points are present at its corners only. It is also called a primitive unit cell.

The total number of atoms in an scc unit cell is z = = 1

Face Centred Cubic Unit Cell FCC: It is that unit Cell in which the lattice points are present at its corners as well as the centre of each face.

A Particle on a face of the cube is shared by 2 faces.

The total no of atoms in an fcc unit cell is z =

Body Centred Cubic unit cell BCC: It is a unit cell in which the lattice points are present in its corners as well as the centre of the body.

The total number of atoms in a bcc unit cell is z =

	Contributes into the Unit Cell
Atoms on Edge	1 / 4
Atoms at Corners	1 / 8
Atoms on Faces	1 / 2
Atoms in the Unit cell	1

Calculation of Density of Unit Cell :

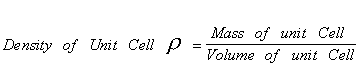
Mass of unit cell = Number of atoms in unit cell x Mass of each atom

Mass of unit cell =

Mass of each atom

Z = No of atoms in unit cell

N is Avogadro’s Number

is the Molar mass of the Crystal

is the volume of the unit cell

Where a is the edge length of a unit cell

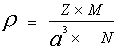
a is the edge length of a cube usually expressed in pico metre or nano metre 1pm =10^-12m and 1nm = 10^-9m

M is the molar mass of the element,

Calculation of the number of Formula units in the NaCl Crystal:

NaCl has FCC type of Unit cell.

The Unit Cell has 12 Edges, 6 Faces and 8 Corners

Na⁺ ions are present at the centre of the cube and on the 12 edges.

No. of Na⁺ions contributed into unit cell by the Edges is ¼ x 12 = 3 ions.

No. of Na⁺ ions in the centre of the unit cell is = 1

Total no. of Na⁺in the Unit Cell is = 3 + 1 = 4

Cl^- ions are present on the 6 Faces and 8 Corners

No. of Cl^-ions contributed into unit the cell by the 6 faces are ½ x 6 = 3

No of Cl^- ions contributed into the unit cell by the 8 corners are 1/8 x 8 = 1

Total No. of Cl^- ions present in the unit cell are 3 + 1 = 4

Therefore there are 4 formula units of NaCl in its unit cell.

Determination of radius of an atom in an Octahedral Void

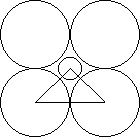
Derive a relationship between the radius r of an atom that can be placed in the

octahedral void constituted by atoms of radius R. (r = .414R)

(BC)² = (AB)²+ (AC)²

(2R)² = (r + R)²⁺+ (r + R)²

(2R)² = 2 (r + R)²

(√2 R)² = (r + R)²

√2 R = r + R

r = √2 R - R

r = R(√2 - 1)

r = R(1.414 - 1)

r = .414R

Radius Ratio Effect

The ratio of the radius of positive and negative ions is known as radius ratio.

The effect of this number in determining the co-ordination number and the shape of an ionic solid is known as radius ratio effect.

Limiting Radius Ratio:-

In a binary compound AB e.g. NaCl, CsCl, ZnS etc.

The co-ordination number of A⁺ is equal to the co-ordination number of B^-.

In Binary AB₂ type of compound CaF_2,CaCl₂ etc.

The co-ordination number of A⁺ is equal to 2 x co-ordination number of B^-

Radius Ratio =

*Radius Ratio r⁺/r^-*	*Co-ordination Number*	*Structure*	*Example*
1 - 0.732	8	Cubic	CsCl
0.732 - 0.414	6	Octahedral	NaCl
0.414 - 0.225	4	Tetrahedral	ZnS
0.225 - 0.155	3	Trigonal	Boron Oxide

Inter Nuclear Distance:-

Inter Nuclear distance = Ionic radius of Cation + Ionic radius of Anion

Inter Nuclear distance of NaCl type of Crystal i.e. r⁺ + r^-

r_c + r_a =

Inter Nuclear distance of CsCl type of Crystal i.e. r⁺ + r^-

r_c + r_a =

For similar kind of elements the radius of the atoms can be calculated using the following equations:

For Simple Cubic Closed packed structures (scc) a = 2r or r =

For Face Centred Cubic close packed structures (fcc) r =

For Body Centred Cubic closed packed structures (bcc) r =

Imperfections in Solids

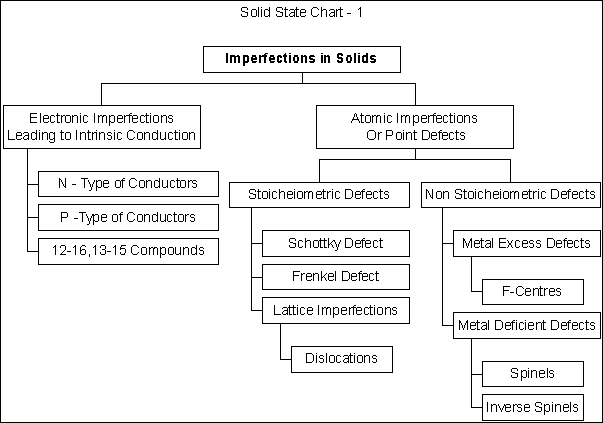
Electronic Imperfections

Intrinsic Conduction: At absolute zero Covalent and ionic compounds have their electrons in the ground state so they do not tend to conduct electric current. At higher temperatures the electrons are released into higher orbitals, creating holes and positive holes. The electrons released in the covalent bonds at higher temperatures in Silicon and Germanium brings about Intrinsic Conduction. The electrons and holes created in the crystals are electronic imperfections.

Semi Conductors

N - Type of Conductors:

The tetravalent silicon and germanium doped with pentavalent group 15 elements e.g. P, As, Sb etc brings about n-type of conduction. The pentavalent impurity has got an unsatisfied valence electron, this free electron can bring about electrical conduction \it is known as an n-type (negative) of conductor. The free electron is the cause for conduction.

P-Type of Conductors:

The tetravalent silicon and germanium doped with trivalent group 13 elements e.g. Al, Ga, In etc. Brings about p-type of conduction. The trivalent impurity cannot complete the three dimensional network of the tetravalent Si or Ge \ this leads to the formation of a Positive hole or electron deficient centre which conducts electricity hence known as p-type of conductor.

12-16 Compounds: When a solid state compound is formed by combination of elements of group 12 and 16 the compounds are called 12 -16 compounds e.g. ZnS, CdS etc. (The effective valency of the two elements become 4 by the combination of the two group elements.)

13 - 15 Compounds: When solid state compounds are obtained by combination of elements of group 13 and 15 the compounds are called 13 - 15 Compounds e.g. AlP, GaAs, InSb etc. (The effective valency of the two elements become 4 by the combination of the two group elements.) These compounds show Solid state properties.

Atomic Imperfections

Point Defects

The imperfections in the crystal due to vacancies in the lattice or due to dislocation of a particle from one position to another position of the lattice is called Point Defect.

Stoichiometric Defects: The compounds in which the numbers of positive and negative ions are exactly in the same ratio indicated by their chemical formula are called stoichiometric compounds.

Schottky Defect

Schottky defect is observed when equal numbers of cations and anions are missing from the lattice. Presence of Schottky defect lowers the density of the solid.(It is a stoichiometric point defect)

Conditions for Schottky defects:

a) The constituent ions should have high Co-ordination number

b) The Cations and Anions Should be almost of same size

c) The compound should be strongly ionic in nature.

Examples: NaCl, KCl, KBr and CsCl.

Frenkel Defect

Frenkel defect arises when a cation leaves its normal lattice site and occupies an interstitial site.

Conditions for Frenkel defect:

a) The constituent ions have low co-ordination number

b) The Anions are much larger than the Cations

Examples: AgBr, AgCl, AgI

What are the consequences of Schottky and Frenkel defects?

· Solids showing these defects conduct electricity to a small extent. This is because if an ion moves from its lattice site to occupy a hole it creates a new hole. In this way a hole moves across the crystal which as a result moves the charge in the opposite direction.

· Due to presence of holes, the stability of the crystal decreases

· In Frenkel defect, similar charges come closer. This results in the increase of dielectric constant of the crystals.

Lattice Imperfections:

Dislocations: When deviation in arrangement of ions extends over microscopic regions they are known as Lattice Imperfections. When a lattice imperfection extends along a line or plane the defect is also known as Dislocation.

Non stoichiometric Defects:

The compounds in which the numbers of positive and negative ions are not exactly in the same ratio indicated by their chemical formula are called stoichiometric compounds.

Metal Excess Defects.

F-Centre When alkali metal halides are heated in an atmosphere of alkali metal vapours, Anion Vacancies are produced. Electrons trapped in anion vacancies are known as F-Centres.

F-Centres are paramagnetic due to the presence of unpaired electrons.

Spinals:

A group of mixed metal oxides with the general formula AB₂O₄ where ‘A’ is divalent and ‘B’ is Trivalent. Where ‘A’ and ‘B’ can be the same or different ‘A’ can be Mg, Fe, Co, Ni, Zn and ‘B’ can be Al, Fe, Mn, Cr or Rh. The Oxygen has cubic closed packed arrangement. In Normal Spinals ‘A’ occupies Tetrahedral voids and in Inverse spinals ‘B’ occupies half the Tetrahedral voids and the other half is in Ocrahedral voids. E.g. Fe₃O₄, MgO Fe₂O₃ etc.

What are F Centres? Why does ZnO turn yellow on heating? And Why does the it loose it yellow colour on cooling? What kind of defect is it?

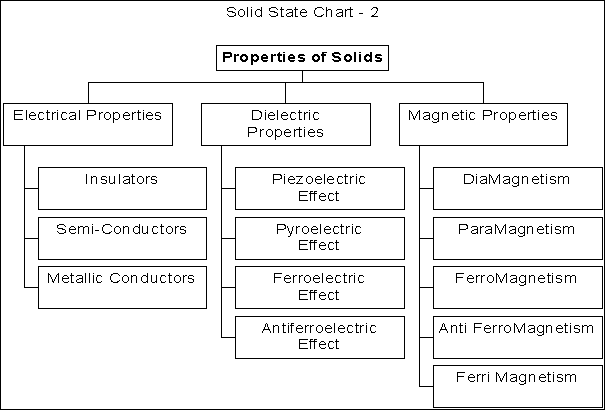
Electrical Properties of Solids:

Semi Conductors: They are solids which are perfect insulators at absolute Zero but conduct current at room temperature.

Insulators are substances whose electrical conductivity is of the order of 10^-12 Ohm^-1 cm^-1 and Conductors are substances whose conductivity is of the order of 10⁶ to 10⁸ Ohm^-1 cm^-1 and Semiconductors conductivity is of the order of 10² to 10^-9 Ohm^-1 cm^-1.

Magnetic Properties:

Paramagnetism:

It is shown by all those substances in which atoms, ions or molecules have unpaired electrons. It is caused by the spin and orbital angular momentum coupling of electrons. Such compounds are weakly attracted by external magnetic fields and the magnetic properties are lost once the external magnetic field is removed. E.g.Oxygen

Diamagnetism:

This property is shown by compounds which do not contain unpaired electrons. These materials are weakly repelled by the external magnetic field. Diamagnetic substances are independent of temperature. e.g. TiO₂, NaCl and Benzene.

Ferromagnetism: áááááá

Substances which are strongly attracted by the magnetic field and show permanent magnetism even when the magnetic field is removed are known as Ferromagnetic Substances.

Ferromagnetism arise due to spontaneous alignment of magnetic moments due to the presence of unpaired electrons

Anti Ferromagnetism: áâáâáâ

If the alignment of magnetic moments in a compound is in a compensatory way so as to give a net magnetic moment of Zero due to the cancellation of the individual magnetic moments, the property is referred to as Anti Ferromagnetism.

Ferrimagnetism: ááâááâ

When the Magnetic moments are aligned in parallel and antiparallel directions in unequal numbers resulting in a net magnetic moment the property of the compound is said to be ferrimagnetic. E.g. Fe₃O₄ and spinels

Effect of temperature on the magnetic behaviour:

Due to spin randomisation many compounds become paramagnetic at high temperature. Fe₃O₄ becomes paramagnetic at 850 K

Dielectric Properties

When an insulator is placed under the influence of an external electric field the electrons in the bonds get polarised leading to the formation of a dipole. This leads to the following dielectric properties.

Piezoelectricity

A crystal in which the dipoles arrange themselves in an ordered way such that the crystal has a net dipole moment are said to exhibit Piezoelectric effect.

When a dielectric crystal is subjected to a mechanical strain electrical charges develop on some parts of the crystal and thus a current is produced this current is called Piezoelectricity. The reverse is also true if opposite charges are applied on the faces of the crystal there will be a mechanical strain due to atomic rearrangement. They are therefore called as Electrical Mechanical Transducers E.g. Quartz Crystals.

Ferroelectricity

These are Piezoelectric crystals in which the dipoles are permanently aligned even in the absence of an external electric field. The application of an external electric field can reverse the direction of polarisation. E.g. Barium Titanate BaTiO₃, Rochelle Salt or Sodium potassium Tartarate and Potassium dihydrogen phosphate KH₂PO₄ .

Antiferroelectricity

Crystals in which there is no net dipole moment due to internal compensation since the dipoles within the alternate polyhedra cancel each other. They do not exhibit Ferroelectric character. E.g. PbZrO₃Lead Zirconate.

Pyroelectricity

When a dielectric crystal like Tourmaline is heated some of its faces become electrically charged and thus a small electric current is produced known as Pyroelectricity.

Amorphous Substances

An amorphous solid is a substance whose constituents do not posses a long range orderly arrangement. The orderly arrangement in them is restricted to very short distances which are of the same order of magnitude as the inter atomic distances.

e.g. Glass, Plastic, fused silica etc.

Amorphous substances are

I. Isotropic

II. Does not have definite melting points

III. Does not have definite interfacial angles

Photovoltaics They are amorphous substances viz. Silica which is capable of converting electromagnetic radiation (light)into electrical energy.

Silicates

They are formed by fusing alkali metal carbonates with silica at 1775K The basic building unit in all silicates is the SiO₄ ^4- tetrahedron. The SiO₄ ^4- units are linked together in many ways in which the oxygen atoms of the silicate units are shared between each other in many ways given below.

Orthosilicates, Pyrosilicates or Island silicates, Chain silicates, Ring silicates and Sheet Silicates (2-Dimensional Silicates)

Orthosilicates:

In simple Orthosilicates the SiO₄ ^4- tetrahedron units do not share any of its oxygen atoms with any of the other tetrahedra units. E.g. Willmenite ZnSiO₄, Zircon ZrSiO₄.

Pyrosilicates or Island silicates

In Pyrosilicates one oxygen atom is shared by two silicate units General formula is (Si₂O₇)^6-

E.g. Thortevitite Sc₂[Si₂O₇] and Hemimorphite Zn(OH)₂(Si₂O₇)H₂O

Ring or Cyclic Silicate

It is formed when two oxygen atoms are shared by two silicate units. They have a general formula (SiO₃^2-)_n examples are Beryl Be₃Al₂Si₆O₁₈ and Wollastonite Ca₃Si₃O₉ both containing 6 six silicate unit ring system. Examples of three silicate unit ring systems are Benitoite BaTi(Si₃O₉).

Chain Silicates

When two oxygen atoms per SiO₄ tetrahedra are shared by other silicate units two kinds of chain silicates are formed. General Formula (SiO₃^2-)_n

I. Pyroxenes They contain a single stranded chain e.g. Enstatite MgSiO₃, Spodumene [Li Al(SiO₃)]

II. Amphiboles They contain a double stranded chain it is present in Asbestos Ca Mg₃O(Si₄O₁₁) and Tremolite Ca₂Mg₅(Si₄O₁₁)₂ (OH)₂.

Sheet Silicates

There are Two kinds 2D and 3Dimensional sheet silicates

2Dimensional silicates are present in Clay each silicate unit shares 3 of its oxygen atoms with three other silicate units giving an infinite sheet structure General formula (Si₂O₅^2-)_n . E.g Talc Mg₃(OH)₃Si₄O₁₀.

3Dimensional Silicates Quartz is an example all the four oxygen atoms of the silicate unit is shared by all the four silicate units surrounding it giving rise to an infinite 3D arrangement. E.g Zeolites NaAlSi₂O₆.